线性代数

矩阵

定义

矩阵是一个由行和列组成的矩形数组，用于表示线性变换或线性方程组。矩阵中的每个元素可以是实数、复数或其他数值类型。

注：

有理数：可以表示为两个整数之比的数（分数），如 1/2 或 -3。包括整数、有限小数和无限循环小数。

无理数：不能表示为两个整数之比的数。这些数的十进制表示是无限不循环小数，如 π和 √2​。

实数：包括所有有理数和无理数的数。它们可以用来描述长度、质量、时间等连续变化的量。

复数：

复数可以表示 a + bi, 其中a, b 都是实数， i 是虚数单位，满足 i² = -1

实部：复数 a+bi中的 a 称为实部。

虚部：复数 a+bi 中的 b 称为虚部。

复数的基本运算：

加法：(a + bi) + (c + di) = (a +c) + (b + d)i

减法：(a + bi) - (c + di) = (a - c) + (b - d)i

乘法：(a + bi) x (c + di) = ac + adi + bci + bd x (-1) = (ac - bd) + (ad + bc)i

除法：(a + bi)/(c + di) = (a + bi)(c - di)/(c + di)(c - di) = (ac + bd)(bc - ad)i/c² + d²

复数的共轭：

复数 a + bi 的共轭是 a - bi。复数与其共轭相乘的结果是一个实数：(a + bi)(a - bi) = a² + b²

复数的模：

复数 a + bi 的模（或绝对值）表示为|a + bi|: |a + bi| = √(a² + b²)

矩阵表示方法

一个 m x n 矩阵表示一个有 m 行 n 列的矩阵：

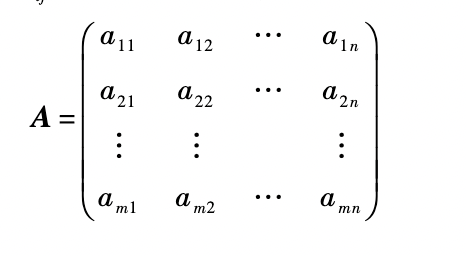
矩阵基本运算

加法：两个同维度的矩阵相加，逐元素相加。

减法：两个矩阵具有相同的维度，然后逐元素相减。

乘法：矩阵乘法不是逐元素相乘，而是行列式的乘积。

转置：矩阵的转置是将矩阵的行变为列，列变为行。

逆矩阵：如果一个矩阵 A 存在逆矩阵 A^-1，则 A × A^-1 = A^-1 × A = I，其中 I 是单位矩阵。（单位矩阵就是对角线上的元素都为1，其它位置的元素都为零）。

注：点击这里，查看更多例子

向量

定义和表示方法

向量指具有大小和方向的量，在几何上可以表示为一个箭头。在线性代数中，向量通常表示为一维数组。根据向量的维度，向量可以是行向量或列向量。

几何意义

几何上，向量表示有方向和大小的量。例如，在二维空间中，向量可以表示一个从原点到点 (x,y) 的箭头。

基本操作

向量空间

向量不仅可以表示为一维数组，还构成了向量空间的基础。向量空间具有以下性质：

• 封闭性：向量的加法和标量乘法结果仍是该向量空间中的向量。
• 零向量：存在一个零向量，使得任何向量加上零向量等于其自身。
• 逆元素：对于每个向量，都存在一个加法逆元，使得两者相加等于零向量。
• 分配律：向量加法和标量乘法满足分配律。

特征值和特征向量

特征向量

特征向量是一个非零向量，当其与一个矩阵相乘时，结果是一个标量倍的自身。换句话说，如果矩阵 A 作用于向量 v，结果是 v 的一个伸缩版本，那么 v 就是 A 的特征向量。

数学上，如果 A 是一个 n×n 的矩阵，v 是一个非零向量，那么 v 是 A 的特征向量，当且仅当存在一个标量 λ，使得：Av = λv

特征值

特征值是与特征向量相关的标量，表示矩阵作用在特征向量上时的伸缩因子。在上面的等式中，λ 就是特征值。

求解特征值和特征向量

特征值的求解：

特征值通过解以下特征方程得到：

Av = λv 推出 Av-λIv = 0推出(A-λI)v = 0，因为v是非零特征向量，所以 det(A−λI) = 零

其中，det⁡ 表示行列式，I 是单位矩阵，λ 是特征值。这个方程也称为特征多项式。

特征向量的求解：

一旦特征值 λ 被找到，将其代入以下方程来求解对应的特征向量 v：

(A−λI)v = 零

注：求解特征值和特征向量的例子